Sistema de Numeración Binario y Quinario

Área: Matemáticas

SISTEMA DE NUMERACIÓN BINARIA

NÚMEROS BINARIOS

  Como ya dijimos, el sistema binario se basa en la representación de cantidades utilizando los números 1 y 0. Por tanto su base es 2 (número de dígitos del sistema). Cada dígito o número en este sistema se denomina bit (contracción de binary digit).

 Por ejemplo el número en binario 1001 es un número binario de 4 bits. Recuerda "cualquier número binario solo puede tener ceros y unos".

 Los Números Binarios empezarían por el 0 (número binario más pequeño) después el 1 y ahora tendríamos que pasar al siguiente número, que ya sería de dos cifras porque no hay más números binarios de una sola cifra. 

 El siguiente número binario, por lo tanto, sería combinar el 1 con el 0, es decir el 10 (ya que el 0 con el 1, sería el 01 y no valdría porque sería igual que el 1), el siguiente sería el número el 11. Ahora ya hemos hecho todas las combinaciones posibles de números binarios de 2 cifras, ya no hay más, entonces pasamos a construir los de 3 cifras. El siguiente sería el 100, luego el 101, el 110 y el 111. Ahora de 4 cifras...

 Según el orden ascendente de los números en decimal tendríamos los números binarios equivalentes a sus números en decimal :

 El 0 en decimal sería el 0 en binario
 El 1 en decimal sería el 1 en binario
 El 2 en decimal sería el 10 en binario (recuerda solo combinaciones de 1 y 0)
 El 3 en decimal sería el 11 en binario
 El 4 en decimal sería el 100 en binario... Mejor mira la siguiente tabla:

 Y así sucesivamente obtendríamos todos los números en orden ascendente de su valor, es decir obtendríamos el Sistema de Numeración Binario y su número equivalente en decimal. 

 Pero que pasaría si quisiera saber el número equivalente en binario al 23.456 en decimal. Tranquilo, hay un método para convertir un número decimal en binario sin hacerlo uno a uno.

 Decimal a Binario

 Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).

 Para sacar la cifra en binario cogeremos el último cociente (siempre será 1) y todos los restos de las divisiones de abajo arriba, orden ascendente.

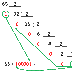
 Ejemplo queremos convertir el número 28 a binario:
28 dividimos entre 2 : Resto 0
14 dividimos entre 2 : Resto 0
 7 dividimos entre 2 : Resto 1
 3 dividimos entre 2 : Resto 1 y cociente final 1

 Entonces el primer número del número equivalente en binario sería el cociente último que es 1 y su resto que es también 1, la tercera cifra del equivalente sería el resto de la división anterior que es 1, el de la anterior que es 0 y el último número que cogeríamos sería el resto de la primera división que es 0.

 Con todos estos número quedaría el número binario: 11100.

 Conclusión el número 28 es equivalente en binario al 11.100.

 Vemos como para sacar el equivalente se coge el último cociente de las operaciones y los restos que han salido en orden ascendente (de abajo arriba) 11100. 

 El subíndice 2 que hemos puesto al final del número en binario, es para indicar que es un número en base 2,  pero no es necesario ponerlo.